时间:2024-05-06 05:42:01
【本章作为我学习最优化模型的笔记汇总篇。会随着我的学习不断的补充最优化模型的总结。包括一些智能优化算法等等】
最优化问题,一般是指在满足一定的约束条件之下(也可能是无约束的问题),使得目标函数取到最优结果。最优结果是自己定义的,可以是最大值,也可以是最小值,或者是区间型等等。
首先,阅读完了《数学建模方法与分析(第四版)Mark M.Meerscheart》有关最优化模型部分,对其内容进行一个提取与整理,并加入我自己的想法与感受。
这本书最优化部分包括了单变量最优化、多变量最优化、最优化的计算方法以及对数学建模五步法和灵敏性分析等相关内容。
首先,我们要分析题目。将题目中涉及的变量都提取出来,最好是能列出一张符号表。
此外,在题目中会明现或者暗含着一些等式或不等式的约束条件,我们需要以数学的形式将这些变量之间的关系给表现出来。
除了题目中涉及的条件,为了简化题目,常常会作出一定的假设。利用这些假设,我们也要写出相关数学表达式。由于是假设,我们先暂且他是正确的,最后进行灵敏性分析我们再对假设进行分析。
最后,利用数学符号表示出我们的目标函数,并且说明好我们最优的结果方向是什么。并且,在建模前,最好将这些写在草稿纸上,以便后续的分析。
在有了一个数学语言表达的问题之后,我们就需要根据我们的所学或者相关的文献资料来确定我们解决问题的模型方法。
对于优化模型一般有:梯度法、拉格朗日乘子法、线性规划法、整数规划法等等。
有时候还需要借助智能优化算法包括:模拟退火算法、免疫算法、粒子算法、蚁群算法、遗传算法等等。这些方法我将在后面具体的介绍。
我们需要将第一步中的数学表达式进行标准化。标准化为我们建模方法所需要的表达式。
也就是说我们要将第一步得到的问题应用于第二步。
开始进行一些求解工作。对于简单的问题可以手动求解。
对于一些计算量大,复杂的问题就需要借助计算机相关软件。例如Matlab、LINGO等等
求解模型出结果后,我们就需要将结果转化为通俗的文字。确保一个毫无建模基础的人,比如说你的领导能听懂你的结果。在这个过程中尽量避免数学符号和术语。
因此最后这一部分是相关重要的,我们需要全面的,严谨的呈现我们的结果。
包括对结果数据的描述,对一些参数的实际意义的阐述,以及我们要进行灵敏性分析来提供出几种可选的方案(基于假设条件的改变,以及加入其他影响因素等等)。
我们所建立的模型很大程度上是基于我们所给出的假设,但是我们并不能保证我们的假设都是完美的。
因此,我们还需要考虑如果假设条件改变,我们所提供的方案或结果是否会发生较大的改变。如果没哟,这就说明了我们模型的稳健性。
如果有,就需要展开说明我们的模型结果还需要进行哪一些方面的补充。从而才能体现我们解决问题的完整性以及全面性,并且可以提高模型的普适性。
除此之外,我们还需要找到模型中的一些核心变量,或者说是不确定变量(容易改变的量)。这些变量是模型的决策变量。虽然有事题目中已经限定了值得大小,但是我们仍然可以看看当值改变后对结果产生的影响(有时候写成百分比改变的形式,这样能更好的体现变量之间的改变关系)即当 时有:
我们称这个相对改变量之比的极限为x对r的灵敏性,一般记为 。
如果影响不大便说明了模型的稳健性,改变较大我们只需要进行解释说明,分析原因即可。
此外,从中也可以发现一些影子价格或者说边际费用等等。这些东西可以为我们模型的适用范围进行一些补充(例如当变量在哪些范围浮动的时候,最优结果不改变等),并且依据影子价格和边际费用可以为决策者提供更好的建议与策略。
补充一点:改变值的时候,我们可以挑选出一些特殊值;也可以直接设置成未知参数,通过绘图可视化来进行分析。
对于单变量最优化问题可以视为利用高等数学知识求解一元函数的最值问题。
也就是说,我们利用数学建模五步法得出来的目标函数是求解一元连续函数的最值,而约束条件一般是将可行解约束到一定的范围之内。
对于求解最值问题,我们可以利用求导的方法,找出极值点,再和临界点比较从而寻找到目标函数的最值。
对于没有约束的最优化,我们可以利用高等数学中求解多元函数的最值方法来求解问题。即:
也就是使梯度为0,即
在进行求解参数之间的灵敏性 时:如果遇到一元函数的灵敏性S求解,利用公式:
如果遇到二元函数的灵敏性S求解,我们可以通过联立方程转化为一元函数,这一般计算量会大,需要借助计算机。但是我们也可以采用多变量函数的链式法则:
其中,
一般求解多元函数最值需要满足:
因此可以化简为:
从而可以求解出变量之间的灵敏性S
对于一些有约束的多变量最优化问题,我们考虑使用拉格朗日乘子法来求解:
对于 ,约束条件(只考虑等式约束情况)可以写为:
在满足上面的条件求解目标函数:
的最大值。一个定理保证了 ,有:
其中
称为拉格朗日乘子 ;
为线性无关向量(需要先检查是否存在异常点)
因此展开写可以得到:
以及约束条件:
几何原理就是 与S垂直,因此
在由 k个向量
所张成的空间中。
当含有不等式的约束条件的时候:
可以通过拉格朗日乘子法和无约束问题的求解方法的组合来解决。即将集合看成两个子集的并集。
对于只有等式约束的,我们按照正常的拉格朗日乘子法求解即可。
对于含有不等式约束的,我们需要根据几何分析来确保此时不存在局部最值或者确保最优解在临界条件上。
对于导数 具有实际意义,为影子价格。并且拉格朗日乘子就是影子价格(待会会证明)。
影子价格实际上是对于每增加单位某一指标参数的量,对应另外一个参量变化的多少。
如每增加一个单位的生产能力,会带来的利润增加额为x,则称x为影子价格。
它代表了某种资源的生产能力(价值)
对于影子价格的求解,实际上是就是求解拉格朗日乘子,接下来给出推导:
,在约束条件:
求解最优值。假设我们最优值发生在
处,也就是说在这个点处拉格朗日乘子的条件是满足的:
我们只需要证明
是影子价格即可,后面的同理可得。我们设x(t)的集合为
上的最优点(此时把
用变量t替代了)。因为有
,故复合函数求导有:
特别的有
,并且对于i=2,3......,k有:
因影子价格为在点
的:
因此: 得证。
另外有关灵敏度分析需要额外补充的一点:
由于 是朝着增长最快的方向,如果改变参数得出的最优结果与原来最优结果所成直线与
垂直。那么我们可以视为变化不大,即不敏感。从而说明了即使参数有了一定的改变,模型给出的结果也是非常接近最优解的

【涉及软件】
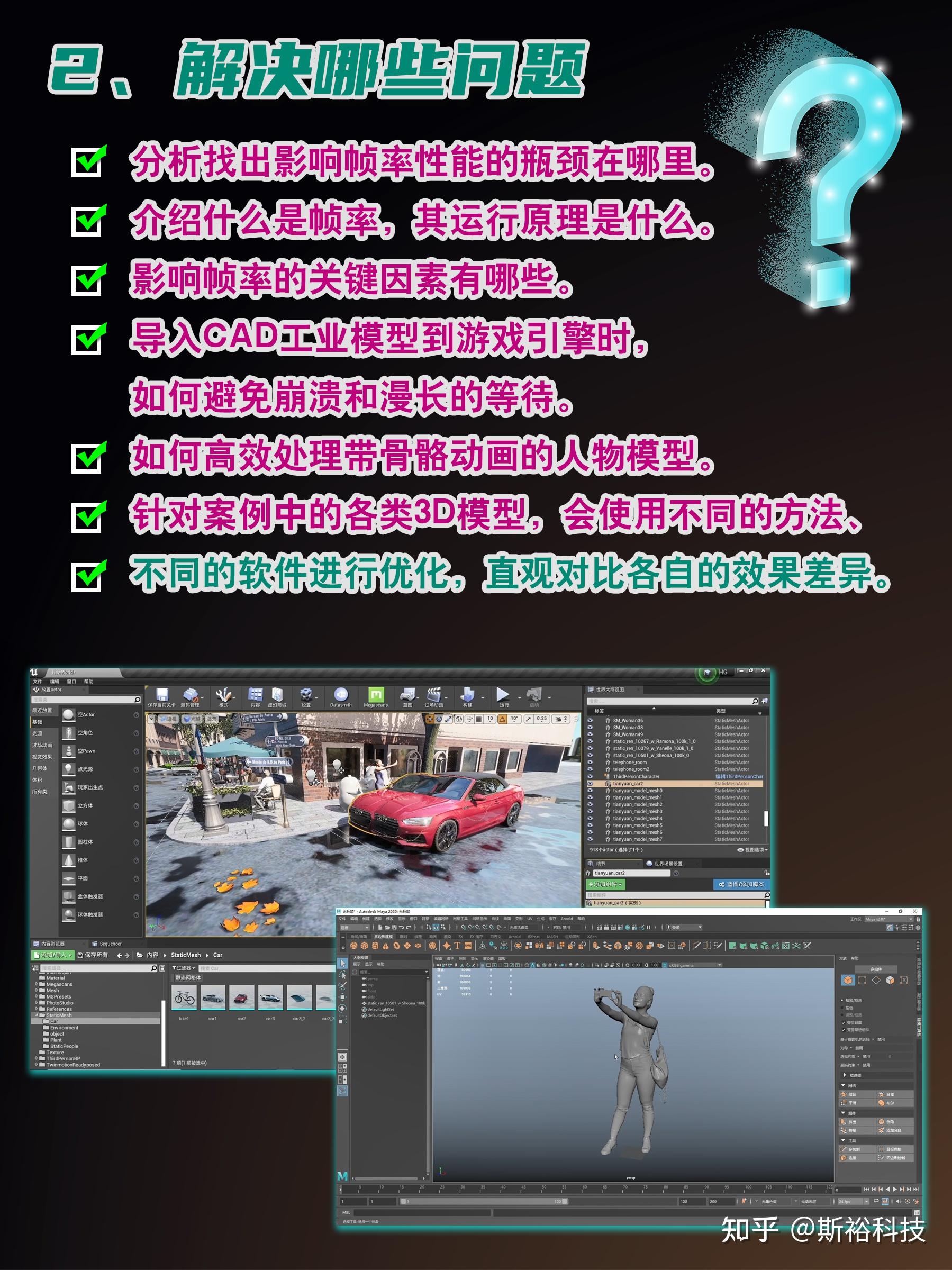
本套教程从设计师做过的项目中总结出模型优化的经验方法,涉及用到各种主流软件、插件工具,包括 3Dmax、Maya、Blender、InstaLOD插件、天元轻量化引擎等等。
【场景案例】
将会用到一个数千万面数级别的街区场景进行演示,该场景里面包含了多个种类的3D模型素材,包括商业建筑群、街道绿化树木、花草植被、公共设施、装饰品,还有一些带动画的行人、静态的人物,还有高精度细节的小轿车以及自行车模型等。
【解决问题】
在这过程中,将会向大家展示具体用什么方法来处理这些模型、每一步的操作是怎么样进行的。解决的具体问题主要包括:
1、分析找出影响帧率性能的瓶颈在哪里。
2、介绍什么是帧率,它的运行原理是什么,影响帧率的关键因素有哪些。
3、对模型进行轻量化处理时,我们需要注意。
4、如何兼顾3D模型总面数的减少和其它方面的关键因素。
5、遇到需要导入CAD工业模型到游戏引擎时,如何避免崩溃和漫长等待,快速得到一个比较满意的模型效果。
6、如何高效处理带骨骼动画的人物模型。
针对案例中的各类3D模型,使用不同的方法、不同的软件工具来进行优化处理,对比使用各种插件工具的效果差异。
本套课程非常适合从事制作游戏、AR/VR、实时渲染类项目的小伙伴观看。