
时间:2024-05-26 09:50:29
到现在也读过几篇拓扑优化的入门文章了,也试着注解过几篇代码。我目前见到的大部分的拓扑优化代码都是基于MATLAB来写的,一来利用矩阵运算可以提高计算效率,二来MATLAB可以和各种CAE软件进行对接,实现二次开发。
MATLAB给我的感觉就是矩阵运算的功能十分强大,利用短短的几行代码就可以替代for循环的那么一大长串,使得代码更加简练。但这也带来了一个问题就是,过于凝练的代码使得我们再复现出相应的内容实现方式就不那么容易。
当然,鱼和熊掌不可兼得,既然代码紧凑好看,那就要多花一番功夫去细细品味它。我之前也倒是都一步步地分析注解过。但无奈本人老喜欢忘事,所以,我就想在这里总结一下这些拓扑优化代码中的有限元分析部分实现方式,也算是一个小总结吧。
下面我将对三篇文章中程序的有限元分析部分进行分析总结,前两篇是基于变密度法的拓扑优化研究,第三篇是基于参数化水平集方法的拓扑优化研究。对于有限元分析部分而言,这几篇文章都大同小异,区别只是在构造方式和运算效率上。这三篇文章分别是:
[1]Sigmund O . A 99 line topology optimization code written in Matlab[J]. Structural & Multidisciplinary Optimization, 2001, 21(2):120-127.
[2]Andreassen E , Clausen A , Schevenels M , et al. Efficient topology optimization in MATLAB using 88 lines of code[J]. Structural & Multidisciplinary Optimization, 2011, 43(1):1-16.
[3]Wei P , Li Z , Li X , et al. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions[J]. Structural & Multidisciplinary Optimization, 2018.
由于这几篇文章都是偏向于算法类,因此研究的算例基本都是最小应变能的梁结构拓扑优化问题,使用的都是比较简单的矩形单元。所以下面我主要讲的是单元节点的编号方式及其实现过程中的某些变量的定义方式。
谈到拓扑优化,自然绕不开本领域的经典之作——O. Sigmund教授的“99行代码”,无论是你以后要研究的是变密度法还是水平集方法,通过这篇《A 99 line topology optimization code written in Matlab》来入门拓扑优化,都是一个不错的选择。那就让我们先从这篇最为经典的文章开始讲起吧。
%%%%%%%%%% FE-ANALYSIS %%%%%%%%%%%%
66 function [U]=FE(nelx,nely,x,penal)
67 [KE] = lk;
68 K = sparse(2*(nelx+1)*(nely+1), 2*(nelx+1)*
(nely+1));
69 F = sparse(2*(nely+1)*(nelx+1),1); U =
sparse(2*(nely+1)*(nelx+1),1);
70 for ely = 1:nely
71 for elx = 1:nelx
72 n1 = (nely+1)*(elx-1)+ely;
73 n2 = (nely+1)* elx +ely;
74 edof = [2*n1-1; 2*n1; 2*n2-1; 2*n2; 2*n2+1;
2*n2+2;2*n1+1; 2*n1+2];
75 K(edof,edof) = K(edof,edof) +
x(ely,elx)^penal*KE;
76 end
77 end99行里的单元编号方式是从左到右按列排布,实现方式也比较简单。首先通过两个嵌套的for循环确定左上角和右上角的节点编号n1,n2。依据这两个编号,分别确定单元的四个节点自由度编号。之后根据材料模型和单元节点自由度编号组装整体刚度矩阵K。后面构造相应的力向量F,根据KU=F来求解位移向量。具体分析流程请参照下文中的注释:
Mistscut:变密度法99行程序注解7 %% PREPARE FINITE ELEMENT ANALYSIS
8 A11 = [12 3 -6 -3; 3 12 3 0; -6 3 12 -3; -3 0 -3 12];
9 A12 = [-6 -3 0 3; -3 -6 -3 -6; 0 -3 -6 3; 3 -6 3 -6];
10 B11 = [-4 3 -2 9; 3 -4 -9 4; -2 -9 -4 -3; 9 4 -3 -4];
11 B12 = [ 2 -3 4 -9; -3 2 9 -2; 4 9 2 3; -9 -2 3 2];
12 KE = 1/(1-nu^2)/24*([A11 A12;A12' A11]+nu*[B11 B12;B12' B11]);
13 nodenrs = reshape(1:(1+nelx)*(1+nely),1+nely,1+nelx);
14 edofVec = reshape(2*nodenrs(1:end-1,1:end-1)+1,nelx*nely,1);
15 edofMat = repmat(edofVec,1,8)+repmat([0 1 2*nely+[2 3 0 1] -2 -1],nelx*nely,1);
16 iK = reshape(kron(edofMat,ones(8,1))',64*nelx*nely,1);
17 jK = reshape(kron(edofMat,ones(1,8))',64*nelx*nely,1);88行作为99行的改进版,在有限元分析的实现方式中有了很大的改变。单元的编号方式其实和99行类似,但是这里弃用了嵌套的for循环,改用MATLAB中的repmat()函数、kron()函数等来实现单元的编号。
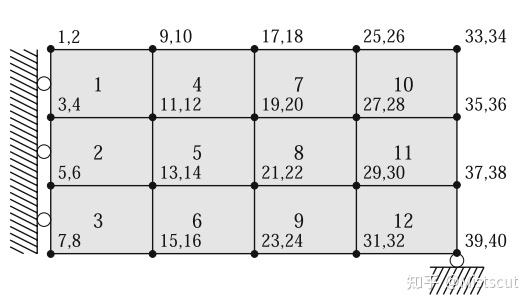
8-12行是组装矩形单元刚度矩阵,值得注意的是,此处单元刚度矩阵KE的编排方式决定了单元的自由度编号顺序一定是逆时针的。
13行借助reshape()函数构造nodenrs矩阵保存节点编号,按列从左往右,从上往下排列,
nodenrs =
1 5 9 13 17
2 6 10 14 18
3 7 11 15 19
4 8 12 16 2014行同样借助reshape()函数,从nodenrs矩阵中提取每一个单元的左上角节点编号,并计算左下角节点的自由度编号(单元的第一自由度,从左下角开始编号)
edofVec =
3
5
7
11
13
15
19
21
23
27
29
3115行通过repmat()函数构造edofMat矩阵,用于储存单元的自由度编号,每一行即为从单元左下角开始,逆时针顺序,得到的单元自由度编号。repmat()函数的作用是平铺矩阵,本行中用到了两次,第一次repmat()的作用是将单元的左下角自由度向量edofVec平铺为1行8列矩阵(nelx*nely,8),可以理解为在8列中的每一列都为edofVec。第二次repmat()的作用是构造单元的每个节点的自由度相较于第一个节点自由度的差值矩阵(nelx*nely,8)。逆时针顺序,差值分别为:左下角(0,1)——>右下角(2*nely+2, 2*nely+3)——>右上角(2*nely, 2*nely+1)——>左上角(-2,-1)。
rep1 =
3 3 3 3 3 3 3 3
5 5 5 5 5 5 5 5
7 7 7 7 7 7 7 7
11 11 11 11 11 11 11 11
13 13 13 13 13 13 13 13
15 15 15 15 15 15 15 15
19 19 19 19 19 19 19 19
21 21 21 21 21 21 21 21
23 23 23 23 23 23 23 23
27 27 27 27 27 27 27 27
29 29 29 29 29 29 29 29
31 31 31 31 31 31 31 31
rep2 =
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
0 1 8 9 6 7 -2 -1
edofMat =
3 4 11 12 9 10 1 2
5 6 13 14 11 12 3 4
7 8 15 16 13 14 5 6
11 12 19 20 17 18 9 10
13 14 21 22 19 20 11 12
15 16 23 24 21 22 13 14
19 20 27 28 25 26 17 18
21 22 29 30 27 28 19 20
23 24 31 32 29 30 21 22
27 28 35 36 33 34 25 26
29 30 37 38 35 36 27 28
31 32 39 40 37 38 29 30第16,17行借助kron()函数提取整体刚度矩阵中的自由度编号。kron()函数是求Kronecker (克罗内克)张量积:如果 A 是 m×n 矩阵,而 B 是 p×q 矩阵,则 A 和 B 的 Kronecker 张量积是通过将 B 乘以 A 的各元素形成的一个大型矩阵。
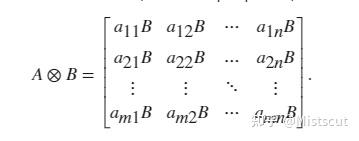
进而iK可以看作是每一个元素被扩充为8行1列,jK可以看作是每个元素扩充为1行8列,由于reshape()函数是按列对矩阵进行重构的,所以在加了转置符号(')之后,即可看作是对行进行重构操作,因此iK为单元自由度编号一组依次重复8次的列矩阵,jK为单元自由度编号单个依次重复8次,最后每一个单元的信息都是占据64行。
因此,在组装整体刚度矩阵的时候,只要分别调用iK和jK对应的值,就是实现了一个单元刚度矩阵KE在整体刚度矩阵K中的对应位置的遍历,进而可以依据材料模型赋予相应的值。
55 K = sparse(iK,jK,sK); K = (K+K')/2;其余的部分就和99行很类似了,此处不再赘述。88行相比99行省去了许多for循环,改用矩阵运算,有效提高了计算的效率,迭代的时候显而易见地要快很多。
参数化水平集88行程序的有限元分析部分整体上和变密度法的88行类似,单元刚度矩阵的定义方式是一样的。唯一的区别就是此处的编号方式是从结构的左下角单元开始编号。
28 eleN1 = repmat((1:nely)',1,nelx)+kron(0:nelx-1,(nely+1)*ones(nely,1));
29 eleNode = repmat(eleN1(:),1,4)+repmat([0,nely+[1,2],1],nelx*nely,1);
30 edofMat = kron(eleNode,[2,2])+repmat([-1,0],nelx*nely,4);
31 iK = reshape(kron(edofMat,ones(8,1))',64*nelx*nely,1);
32 jK = reshape(kron(edofMat,ones(1,8))',64*nelx*nely,1); 第28行通过repmat()函数和kron()函数获取单元的第一个节点编号矩阵eleN1,其中repmat()函数是将第一列的节点编号按列排布nelx份;kron()函数是构造每一列单元第一节点编号和第一列的差值矩阵。二者组合之后即为单元的第一节点编号矩阵:
rep =
1 1 1 1
2 2 2 2
3 3 3 3
kr =
0 4 8 12
0 4 8 12
0 4 8 12
eleN1 =
1 5 9 13
2 6 10 14
3 7 11 15
第29行通过两个repmat()函数来构造节点矩阵eleNode,第一个repmat()函数将转化为列向量的单元第一节点编号矩阵eleN1平铺4份生成(nelx*nely,4)大小的矩阵;第二个repmat()函数构造第一节点编号差值矩阵(nelx*nely,4),二者相加即单元节点编号矩阵eleNode,每一行即为一个单元的节点编号。
rep1 =
1 1 1 1
2 2 2 2
3 3 3 3
5 5 5 5
6 6 6 6
7 7 7 7
9 9 9 9
10 10 10 10
11 11 11 11
13 13 13 13
14 14 14 14
15 15 15 15
rep2 =
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
0 4 5 1
eleNode =
1 5 6 2
2 6 7 3
3 7 8 4
5 9 10 6
6 10 11 7
7 11 12 8
9 13 14 10
10 14 15 11
11 15 16 12
13 17 18 14
14 18 19 15
15 19 20 16第30行通过repmat()函数和kron()函数来构造和变密度法88行中相同的节点自由度编号矩阵edofMat。kron()函数将每一行的每一个节点扩充为2列,并乘2,即构造2*N; repmat()函数将-1和0分别平铺到1行8列,分别对应x和y方向的自由度。二者相加即可构造一个单元的节点自由度矩阵。
edofMat =
1 2 9 10 11 12 3 4
3 4 11 12 13 14 5 6
5 6 13 14 15 16 7 8
9 10 17 18 19 20 11 12
11 12 19 20 21 22 13 14
13 14 21 22 23 24 15 16
17 18 25 26 27 28 19 20
19 20 27 28 29 30 21 22
21 22 29 30 31 32 23 24
25 26 33 34 35 36 27 28
27 28 35 36 37 38 29 30
29 30 37 38 39 40 31 32注意:由于单元矩阵的构造方式与变密度法88行相同,单元的编号方式也是逆时针的。虽然看起来从左上角开始编号好像也可以对应起来,但其实编号方式还是从左下角开始的。
第31,32行与变密度法88行相同,此处不再赘述。
在材料模型上,由于水平集方法要切割边界单元,因此在边界单元的处理上要额外计算单元的有效体积,其余的分析流程和上述两篇文章大体相同。
刚开始入门的时候被这些矩阵运算搞得云里雾里,在学习一段时间之后也渐渐地有了一些感悟和收获。虽然这只是一些较为简单的有限元分析过程,涉及到的只是矩形单元和应变能问题。但我觉得学习前辈们的编程思维和编程方法对之后进一步的研究工作还是很有帮助的。
—— 2021.05.17 Mist 于 五山