? ? ? 在上一篇博客 粒子群优化算法（1）中介绍了基本的粒子群算法，基本粒子群算法是基于连续空间（区间）进行搜索，然而在一些实际的工程应用中，我们的待求解的变量可能并不是历需的，而实一种离散型的变量。这就需要对基本的粒子群算法做出一些相应的改进。

? ? ? 在离散粒子群算法中，将离散问题空间映射到连续粒子运动空间，并做适当的修改。任然保留经典粒子群算法的速度-位置更新策略。粒子在状态空间的取值只限于0，1两个值，而速度的每一个位代表的是粒子位置所对应的位取值为0/1的可能性。因此在离散粒子群算法中，粒子速度的更新公式依然保持不变，但是个体最优位置和全局最优位置每一位的取值只能为0/1。

? ? ? 离散粒子群算法速度和位置的更新方式如下所示：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? 粒子速度的更新方式不变，但是其位置的更新方式如下所示：

? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? (利用sigmoid函数将例子的速度映射到0-1之间)

? ? ? 则粒子的速度可以表示为：

? ?

例如，对于经典的0-1背包问题：如果采用粒子群优化算法求解，只能是采用离散的粒子群算法：
问题描述：

有一个容量为V的背包，有N件物品，第i件物品的体积是c(i),价值是w(i).那么将哪些物品放入背包中，可以使得价值最大。假设具体的数据如下：

假设N=10, V = 300, 每件物品的体积为：[95, 75, 23, 73, 50, 22, 6, 57, 89, 98], 物品的价值为[89， 59，19, 43, 100, 72, 44, 16, 7, 64]

具体的计算流程如下：

1. 对速度进行初始化，对粒子的位置进行初始化，这里粒子的位置采用的二进制的表示方法。1表示选择该物体，0表示不选择该物体。其他的参数的初始化的过程与前面的方法一样。

源代码：

运行结果：

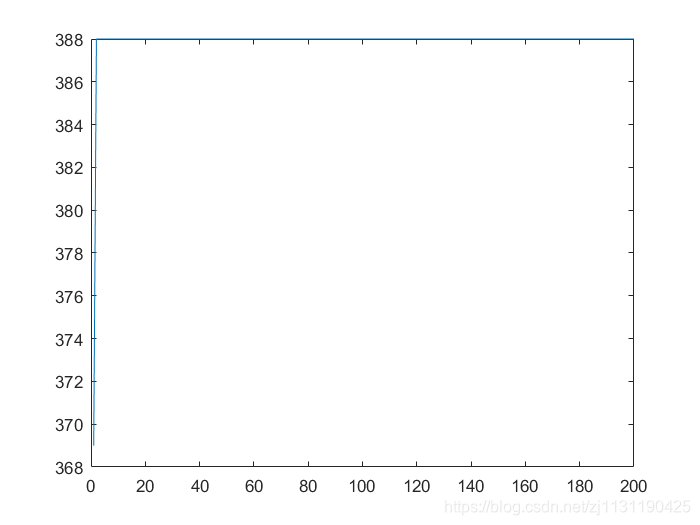
除此之外，还可以使用离散粒子群算法求解单变量的优化问题：
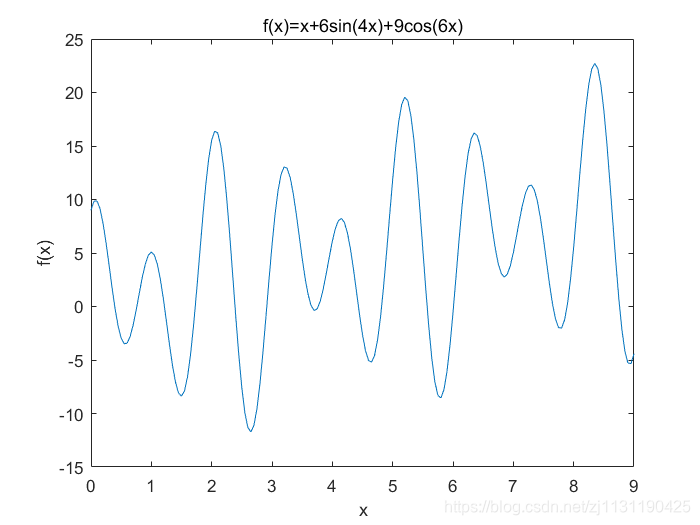
例如，求解函数的极值，函数的表达式如下所示：

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

其中：

可以画出函数的图像，如下所示：

源代码：

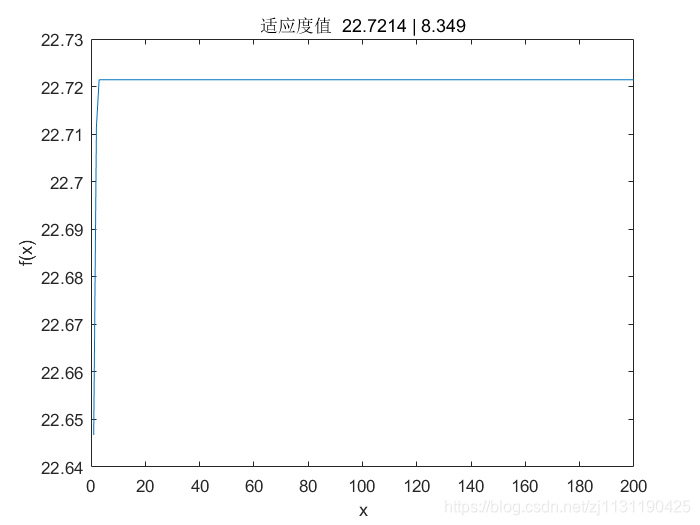
求取最大值，将mode参数设置为‘max’即可：

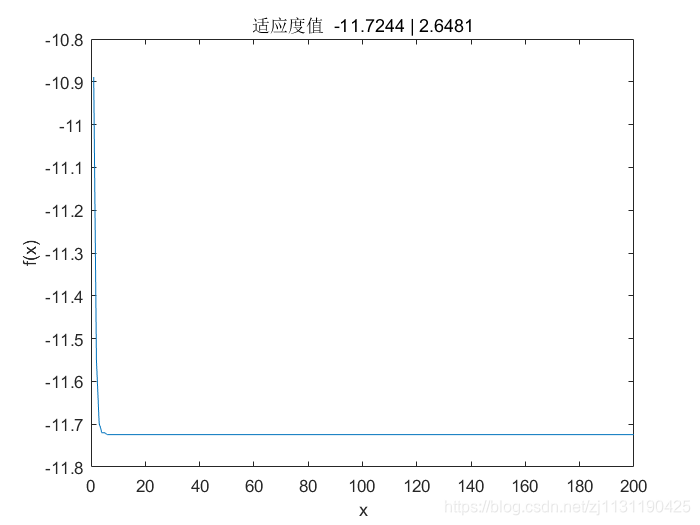
求取最小值，将mode参数设置为‘min’即可：

?